We have postdoctoral positions and fully funded PhD student positions available!

Self-Organization of Multicellular Systems
Self-Organization of Multicellular Systems
Welcome to our group webpage! We are a joint research group between the Max Planck Institute for the Physics of Complex Systems (MPI-PKS) and the Max Planck Institute of Molecular Cell Biology and Genetics (MPI-CBG), based at the Center for Systems Biology Dresden (CSBD), established in 2021.
We are theorists, but we closely collaborate with experimentalists, at MPI-CBG and beyond, on problems in theoretical biophysics, applied mathematics, and soft matter physics. Read more about our research.
Looking for a PhD or postdoc position? Read more about how to join us.
Latest Research
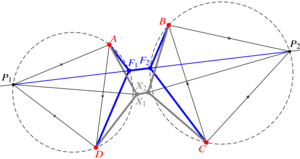
Geometry of T1 transitions in epithelia
Pierre A. Haas#, arXiv (2025)
The flows of tissues of epithelial cells often involve T1 transitions. These neighbour exchanges are irreversible rearrangements crossing an energy barrier. Here, by an exact geometric construction, I determine this energy barrier for general, isolated T1 transitions dominated by line tensions. I show how deviations from regular cell packing reduce this energy barrier, but find that line tension fluctuations increase it on average. By another exact construction, I show how nonlinear tensions in vertex models of epithelial tissues also resist T1 transitions. My results thus form the basis for coarse-grained descriptions of cell neighbour exchanges in continuum models of epithelia.
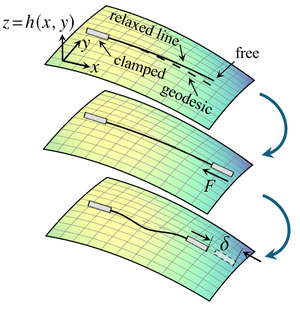
Euler buckling on curved surfaces
Shiheng Zhao and Pierre A. Haas#, arXiv (2025)
Euler buckling epitomises mechanical instabilities: An inextensible straight elastic line buckles under compression when the compressive force reaches a critical value F*> 0. Here, we extend this classical, planar instability to the buckling under compression of an inextensible relaxed elastic line on a curved surface. By weakly nonlinear analysis of an asymptotically short elastic line, we reveal that the buckling bifurcation changes fundamentally: The critical force for the lowest buckling mode is F* = 0 and higher buckling modes disconnect from the undeformed branch to connect in pairs. Solving the buckling problem numerically, we additionally find a new post-buckling instability: A long elastic line on a curved surface snaps through under sufficient compression. Our results thus set the foundations for understanding the buckling instabilities on curved surfaces that pervade the emergence of shape in biology.