When a nonlinearity test is performed with the question in mind if nonlinear deterministic modeling of the signal may be useful, it seems most appropriate to use a test statistic that is related to a nonlinear deterministic approach. We have to keep in mind, however, that a positive test result only indicates nonlinearity, not necessarily determinism. Since nonlinearity tests are usually performed on data sets which do not show unambiguous signatures of low-dimensional determinism (like clear scaling over several orders of magnitude), one cannot simply estimate one of the quantitative indicators of chaos, like the fractal dimension or the Lyapunov exponent. The formal answer would almost always be that both are probably infinite. Still, some useful test statistics are at least inspired by these quantities. Usually, some effective value at a finite length scale has to be computed without establishing scaling region or attempting to approximate the proper limits.
In order to define an observable in m-dimensional phase space, we first have
to reconstruct that space from a scalar time series, for example by the method
of delays:
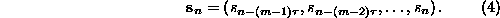
One of the more robust choices of phase space observable is a nonlinear
prediction error with respect to a locally constant predictor
F that can be defined by
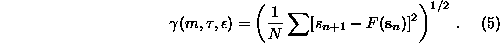
The prediction over one time step is performed by averaging over the future
values of all neighbouring delay vectors closer than 
in m
dimensions.
We have to consider the limiting case that the deterministic signature to be detected is weak. In that case, the major limiting factor for the performance of a statistical indicator is its variance since possible differences between two samples may be hidden among the statistical fluctuations. In Ref. [13], a number of popular measures of nonlinearity are compared quantitatively. The results can be summarised by stating that in the presence of time-reversal asymmetry, the particular quantity Eq.(3) that derives from the three-point autocorrelation function gives very reliable results. However, many nonlinear evolution equations produce little or no time-reversal asymmetry in the statistical properties of the signal. In these cases, simple measures like a prediction error of a locally constant phase space predictor, Eq.(5), performed best. It was found to be advantageous to choose embedding and other parameters in order to obtain a quantity that has a small spread of values for different realisations of the same process, even if at these parameters no valid embedding could be expected.
Of course, prediction errors are not the only class of nonlinearity measures that has been optimised for robustness. Notable other examples are coarse-grained redundancies [14, 15, 16], and, at an even higher level of coarse-graining, symbolic methods [17]. The very popular method of false nearest neighbours [18] can be easily modified to yield a scalar quantity suitable for nonlinearity testing. The same is true for the concept of unstable periodic orbits (UPOs) [19, 20].