

Next: Phase space observables
Up: Detecting weak nonlinearity
Previous: Detecting weak nonlinearity
Traditional measures of nonlinearity are derived from generalisations of the
two-point auto-covariance function or the power spectrum. The use of higher
order cumulants as well as bi- and multi-spectra is discussed for example in
Ref. [10]. One particularly useful third order quantity is
is
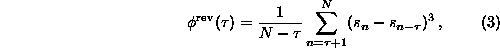
since it measures the asymmetry of a series under time reversal. (Remember that
the statistics of linear stochastic processes is always symmetric under time
reversal. This can be most easily seen when the statistical properties are
given by the power spectrum which contains no information about the direction
of time.) Time reversibility as a criterion for discriminating time series
is discussed in detail in Ref. [11], where, however, a different
statistic is used to quantify it. The concept itself is quite folklore and has
been used for example in Refs. [6, 12].
Time irreversibility can be a strong signature of nonlinearity. Let us point
out, however, that it does not imply a dynamical origin of the nonlinearity.
We will later (Sec. 7.1) give an example of time asymmetry
generated by a measurement function involving a nonlinear time average.


Next: Phase space observables
Up: Detecting weak nonlinearity
Previous: Detecting weak nonlinearity
Thomas Schreiber
Mon Aug 30 17:31:48 CEST 1999
 is
is