The maximal exponent

  The maximal Lyapunov exponent can be determined without the explicit construction of a model for the time series. A reliable characterization requires that the independence of embedding parameters and the exponential law for the growth of distances are checked [69, 70] explicitly. Consider the representation of the time series data as a trajectory in the embedding space, and assume that you observe a very close return to a previously visited point . Then one can consider the distance as a small perturbation, which should grow exponentially in time. Its future can be read from the time series: . If one finds that then is (with probability one) the maximal Lyapunov exponent. In practice, there will be fluctuations because of many effects, which are discussed in detail in [69]. Based on this understanding, one can derive a robust consistent and unbiased estimator for the maximal Lyapunov exponent. One computes
 
If exhibits a linear increase with identical slope for all m larger than some and for a reasonable range of , then this slope can be taken as an estimate of the maximal exponent .

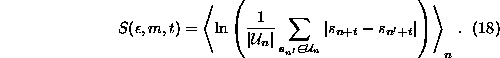
The formula is implemented in the routine lyapunov in a straightforward way. (The program lyap_r implements the very similar algorithm of Ref. [70] where only the closest neighbor is followed for each reference point. Also, the Euclidean norm is used.) Apart from parameters characterizing the embedding, the initial neighborhood size is of relevance: The smaller , the large the linear range of S, if there is one. Obviously, noise and the finite number of data points limit from below. It is not always necessary to extend the average in Eq.() over the whole available data, reasonable averages can be obtained already with a few hundred reference points . If some of the reference points have very few neighbors, the corresponding inner sum in Eq.() is dominated by fluctuations. Therefore one may choose to exclude those reference points which have less than, say, ten neighbors. However, discretion has to be applied with this parameter since it may introduce a bias against sparsely populated regions. This could in theory affect the estimated exponents due to multifractality. Like other quantities, Lyapunov estimates may be affected by serial correlations between reference points and neighbors. Therefore, a minimum time for |n-n'| can and should be specified here as well. See also Sec..

 
Figure:   Estimating the maximal Lyapunov exponent of the CO laser data. The top panel shows results for the Poincaré map data, where the average time interval is 52.2 samples of the flow, and the straight line indicates . For comparison: The iteration of the radial basis function model of Fig.  yields =0.35. Bottom panel: Lyapunov exponents determined directly from the flow data. The straight line has slope . In good approximation, . Here, the time window w to suppress correlated neighbors has been set to 1000, and the delay time was 6 units.

Let us discuss a few typical outcomes. The data underlying the top panel of Fig.  are the values of the maxima of the CO laser data. Since this laser exhibits low dimensional chaos with a reasonable noise level, we observe a clear linear increase in this semi-logarithmic plot, reflecting the exponential divergence of nearby trajectories. The exponent is per iteration (map data!), or, when introducing the average time interval, 0.007 per s. In the bottom panel we show the result for the same system, but now computed on the original flow-like data with a sampling rate of 1 MHz. As additional structure, an initial steep increase and regular oscillations are visible. The initial increase is due to non-normality and effects of alignment of distances towards the locally most unstable direction, and the oscillations are an effect of the locally different velocities and thus different densities. Both effects can be much more dramatic in less favorable cases, but as long as the regular oscillations possess a linearly increasing average, this can be taken as the estimate of the Lyapunov exponent. Normalizing by the sampling rate, we again find 0.007 per s, but it is obvious that the linearity is less pronounced then for the map-like data. Finally, we show in Fig.  an example of a negative result: We study the human breath rate data used before. No linear part exists, and one cannot draw any reasonable conclusion. It is worth considering the figure on a doubly logarithmic scale in order to detect a power law behavior, which, with power 1/2, could be present for a diffusive growth of distances. In this particular example, there is no convincing power law either.

 
Figure:   The breath rate data (c.f. Fig. ) exhibit no linear increase, reflecting the lack of exponential divergence of nearby trajectories.