Nonlinear noise reduction

  Filtering of signals from nonlinear systems requires the use of special methods since the usual spectral or other linear filters may interact unfavorably with the nonlinear structure. Irregular signals from nonlinear sources exhibit genuine broad band spectra and there is no justification to identify any continuous component in the spectrum as noise. Nonlinear noise reduction does not rely on frequency information in order to define the distinction between signal and noise. Instead, structure in the reconstructed phase space will be exploited. General serial dependencies among the measurements 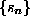will cause the delay vectors 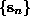to fill the available m-dimensional embedding space in an inhomogeneous way. Linearly correlated Gaussian random variables will for example be distributed according to an anisotropic multivariate Gaussian distribution. Linear geometric filtering in phase space seeks to identify the principal directions of this distribution and project onto them, see Sec. . Nonlinear noise reduction takes into account that nonlinear signals will form curved structures in delay space. In particular, noisy deterministic signals form smeared-out lower dimensional manifolds. Nonlinear phase space filtering seeks to identify such structures and project onto them in order to reduce noise.

There is a rich literature on nonlinear noise reduction methods. Two articles of review character are available, one by Kostelich and Schreiber [57], and one by Davies [58]. We refer the reader to these articles for further references and for the discussion of approaches not described in the present article. Here we want to concentrate on two approaches that represent the geometric structure in phase space by local approximation. The first and simplest does so to constant order, the more sophisticated uses local linear subspaces plus curvature corrections.

 
• Simple nonlinear noise reduction
• Locally projective nonlinear noise reduction
• Nonlinear noise reduction in a data stream