SVD filters

  There are at least two reasons to apply an SVD filter to time series data: Either, if one is working with flow data, one can implicitly determine the optimal time delay, or, when deriving a stroboscopic map from synchronously sampled data of a periodically driven system, one might use the redundancy to optimize the signal to noise ratio.

In both applications the mathematics is the same: One constructs the covariance matrix of all data vectors (e.g. in an m-dimensional time delay embedding space),

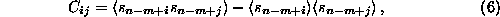
and computes its singular vectors. Then one projects onto the m-dimensional vectors corresponding to the q largest singular values. To work with flow data, q should be at least the correct embedding dimension, and m considerably larger (e.g. m=2q or larger). The result is a vector valued time series, and in [22] the relation of these components to temporal derivatives on the one hand and to Fourier components on the other hand were discussed. If, in the non-autonomous case, one wants to compress flow data to map data, q=1. In this case, the redundancy of the flow is implicitly used for noise reduction of the map data. The routine pca can be used for both purposes.